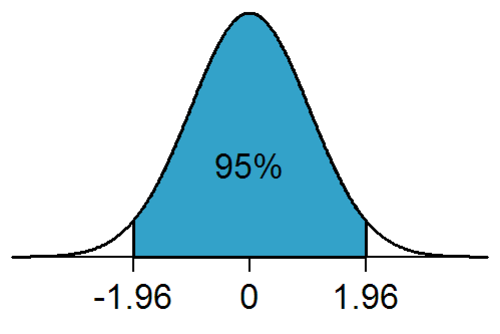
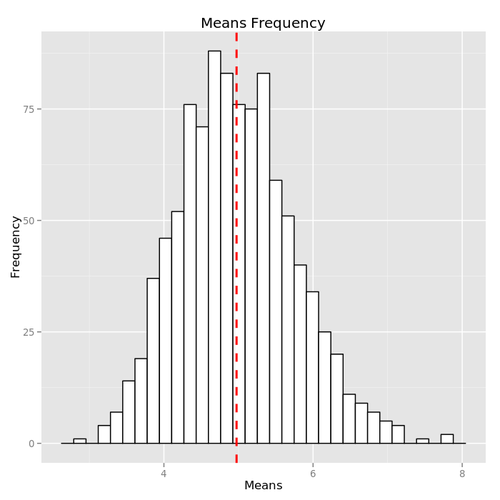
The Central Limit Theorem states that the distribution of sample statistics (e.g. mean) is approximatively normal, regardless of the underlying distribution, with mean = \(\mu\) and variance = \(\sigma^2\) ...

This is my note on swirl course Regression Model : Overfitting and Underfitting.

Definition¶

A variance inflation factor (VIF) is a ratio of estimated variances, the variance due to including the ith regressor, divided by that due to including a corresponding ideal regressor which is uncorrelated with the others. VIF is …

Experimenting the Cental Limit Theorem with R