Confusion Matrix

A confusion matrix, also known as a contingency table or an error matrix or tavle of confusion, is a specific table layout that allows visualization of the performance of an algorithm, typically a supervised learning one (in unsupervised learning it is usually called a matching matrix).

It is a table with two rows and two columns that reports the number of false positives, false negatives, true positives, and true negatives.

For example, for a test that screens people for a given disease, the confusion matrix will be:

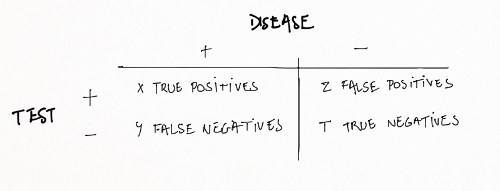
with
x true positives (TP) : the number of sick people correctly identified as sick
z false positives (FP) : the number of healthy people incorrectly identified as sick
t true negatives (TN) : the number of healthy people correctly identified as healthy
y false negatives (FN) : the number of sick people incorrectly identified as healthy

The following probabilities are associated with the confusion matrix:

$Sensitivity = Pr\left(positive\ test\ |\ disease\right)$
$Specificity = Pr\left(negative\ test\ |\ no\ disease\right)$
$Positive\ Predictive\ Value = Pr\left(disease\ |\ positive\ test\right)$
$Negative\ Predictive\ Value = Pr\left(no disease\ |\ negative\ test\right)$
$Accuracy = Pr\left(correct\ outcome\right)$

which are computed the following way:

$$Sensitivity = \frac{TP}{TP+FN}$$

$$Specificity = \frac{TN}{FP+TN}$$

$$Positive\ Predictive\ Value = \frac{TP}{TP+FP}$$

$$Negative\ Predictive\ Value = \frac{TN}{FN+TN}$$

$$Accuracy = \frac{TP+TN}{TP+FP+FN+TN}$$

Examples¶

Example 1 A diagnostic test with sensitivity 67% and specificity 91% is applied to 2030 people to look for a disorder with a population prevalence of 1.48%.

Let's build the associated 2×2 contingency table:

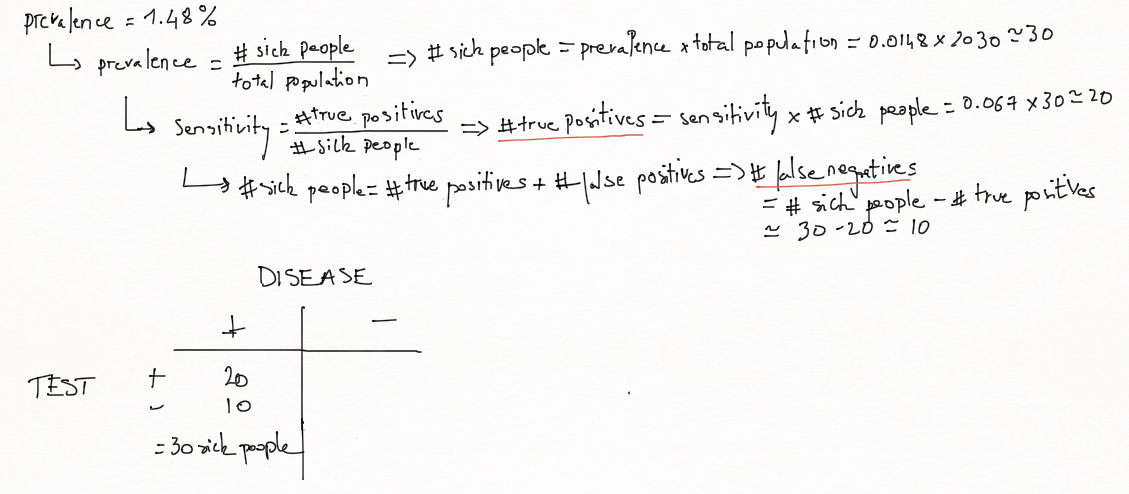
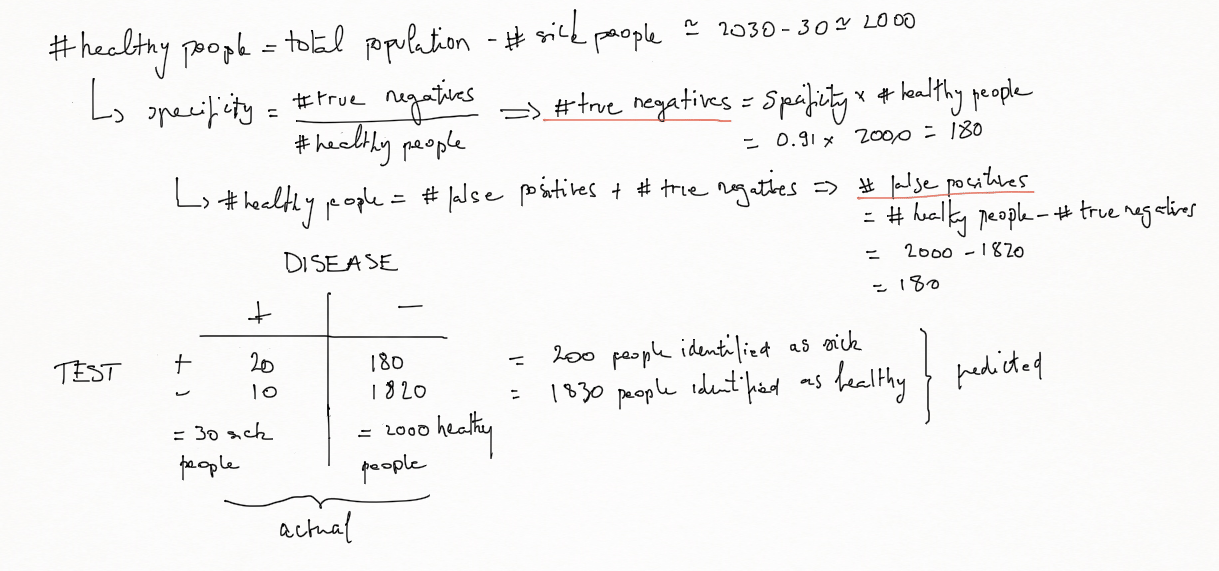
To summary and more simply:

There were 2030 people tested, then 2030 predictions
Out of those 2030 tests, 200 were identified as sick, 1830 as healthy
In reality, 30 people are sick, 2000 are healthy

Example 2 Suppose that we have created a machine learning algorithm that predicts whether a link will be clicked with 99% sensitivity and 99% specificity. The rate the link is clicked is 1/1000 of visits to a website. If we predict the link will be clicked on a specific visit, what is the probability it will actually be clicked?

Let's be 100000 the number of visits:

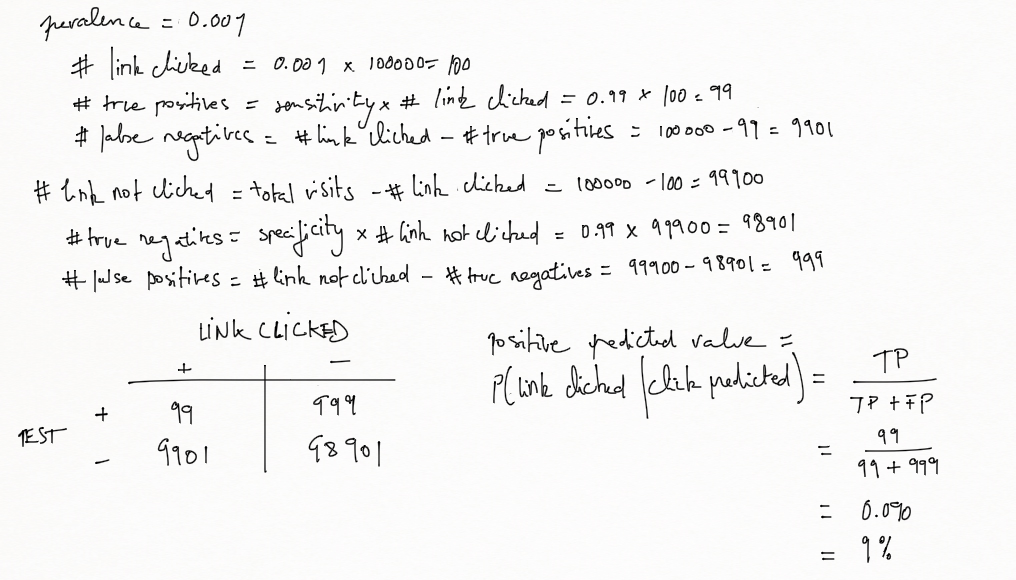
According to the confusion matrix above, the probability that the link will be actually clicked is 9%.